
규칙은 그리 어렵지 않다.
주어진 3개의 점이 만약 일직선상에 놓여있다면 ?
이는 사각형이 만들어질 수 없는 조건이므로 -1.0을 출력한다.
사각형의 둘레를 구하는 것은 좀 더 생각을 해봐야 한다.
나는 모든 경우의 수를 생각하고 일치하는 조건들을 찾는 타입이다.
결국 찾았다.
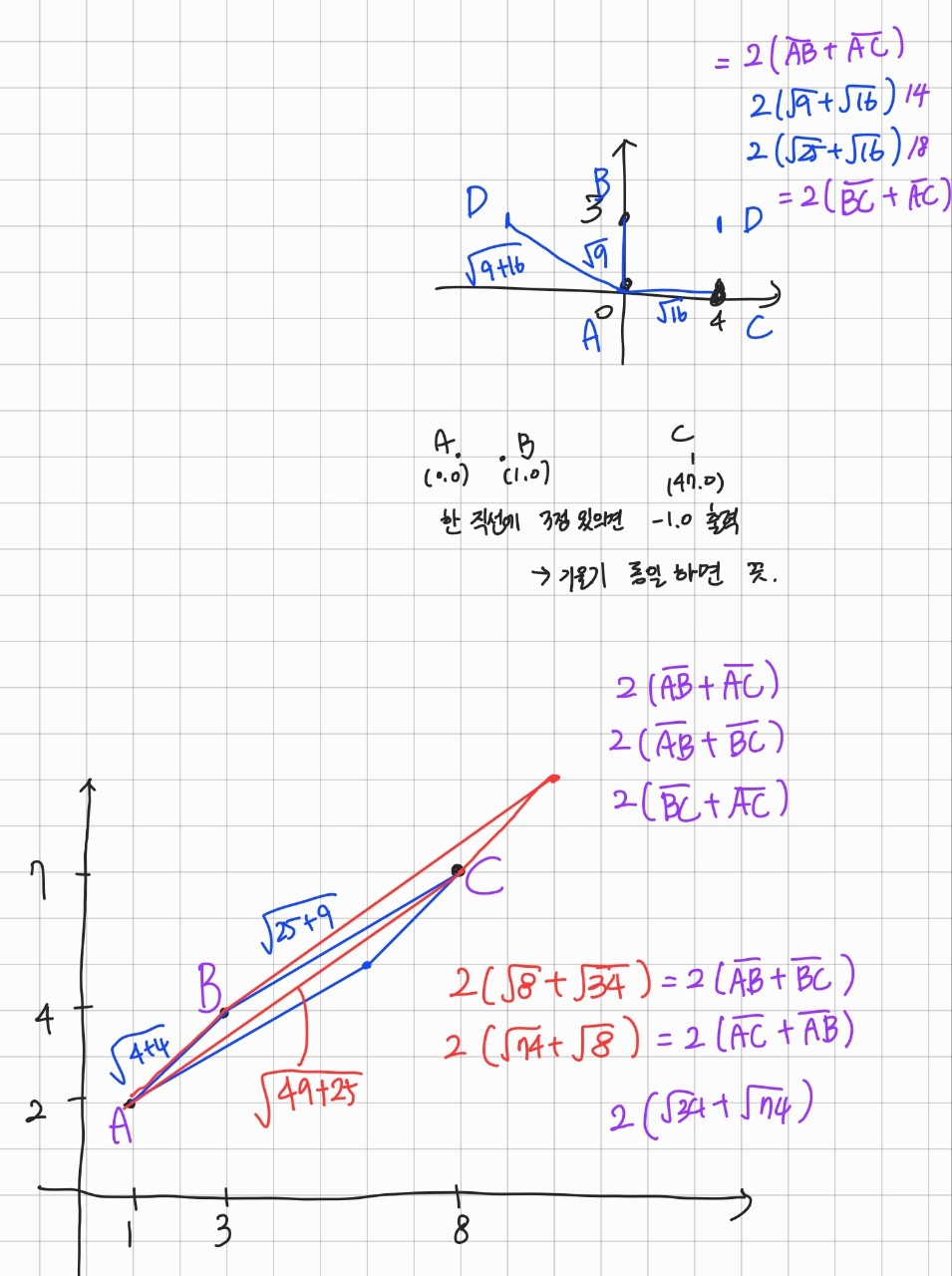
저 보라색으로 쓰여있는 것이 우리가 따져볼 수 있는 둘레의 경우의 수이다.
저기서 최댓값, 최솟값을 구해 차이를 출력하면 되는 문제였다.
두 점 사이의 거리를 구할 때는 피타고라스의 정리가 이용된다.
이는 중학교 때 배운 것이니 코드로 직접 보일 것이다.
소수점의 자리수도 생각해줘야 한다. 기본은 6자리까지밖에 안나오기 때문에 %.16f를 사용하든 cout<<fixed; cout.precision(16)을 설정하여 소수점을 많이 출력되게 만들어 오차를 줄여야 한다.
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
struct xy {
double x;
double y;
};
struct xy xy[3];
bool cmp1(struct xy A, struct xy B) {
if (A.x == B.x) {
return A.y < B.y;
}
return A.x < B.x; // x 오름차순 정렬
}
double PITA(int x1, int y1, int x2, int y2) { // 두 점 사이의 길이
return sqrt((y2 - y1) * (y2 - y1) + (x2 - x1) * (x2 - x1));
}
int main() {
for (int i = 0; i < 3; i++)
{
cin >> xy[i].x >> xy[i].y;
}
sort(xy, xy + 3, cmp1);
if ((xy[0].y - xy[1].y) * (xy[1].x - xy[2].x) == (xy[1].y - xy[2].y) * (xy[0].x - xy[1].x)) {
// 한 직선에 3개의 점이 있으면(기울기가 같으면) 사각형이 만들어 질 수 없음
// 하지만 나눗셈(/)을 쓴다면 division by zero가 발생할 수 있으므로 사용하지 않음
cout << "-1.0";
}
else
{
double AB = PITA(xy[0].x, xy[0].y, xy[1].x, xy[1].y);
double AC = PITA(xy[0].x, xy[0].y, xy[2].x, xy[2].y);
double BC = PITA(xy[1].x, xy[1].y, xy[2].x, xy[2].y);
double sum1 = 2 * (AB + AC);
double sum2 = 2 * (AB + BC);
double sum3 = 2 * (BC + AC);
double maximum = max(sum3, max(sum1, sum2));
double minimum = min(sum3, min(sum1, sum2));
printf("%.16lf", (maximum - minimum));
}
}정말 어이없게 처음에 구조체에서 double이 아닌 float를 써서 계속 틀렸다..

'백준' 카테고리의 다른 글
| [2512] 예산 (0) | 2022.09.27 |
|---|---|
| [1094] 막대기 (0) | 2022.09.27 |
| [1904] 01타일 (0) | 2022.09.25 |
| [9184] 신나는 함수 실행 (0) | 2022.09.23 |
| [14889] 스타트와 링크 (0) | 2022.09.21 |




댓글